Partial-to-Partial Shape Matching with Geometric Consistency

CVPR, 2024

Viktoria Ehm1,2 Maolin Gao1,2 Paul Roetzer3 Marvin Eisenberger1,2 Daniel Cremers1,2 Florian Bernard3
1TUM 2Munich Center for Machine Learning 3University of Bonn
Paper Code Video

We present the first geometrically consistent partial-to-partial shape matching solution. Our approach can find correspondences between partial shapes and thus determine the overlapping region between these shapes (left). We can find correspondences within shape classes (middle), and across shape classes (right). For the latter, we introduce a new inter-class partial-to-partial matching dataset.

Abstract

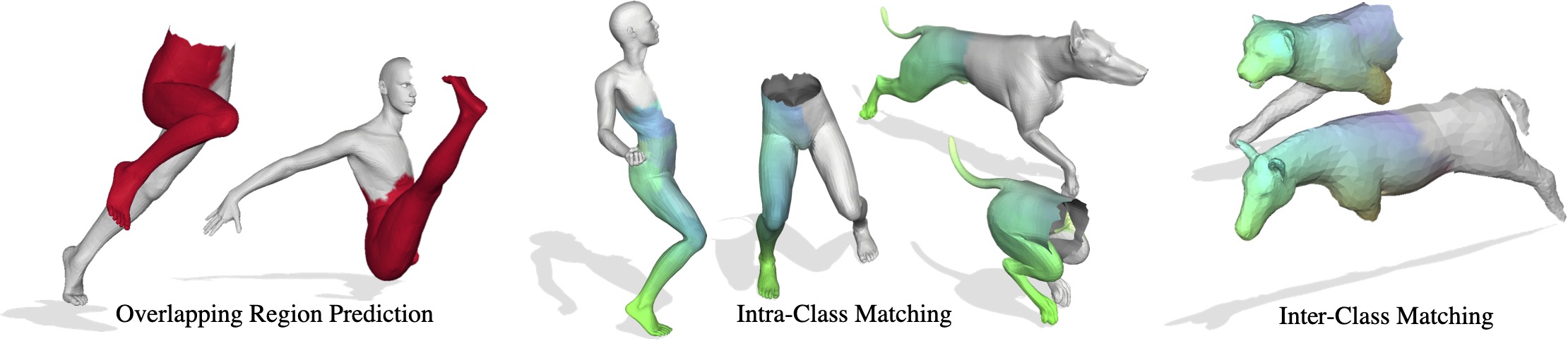
Finding correspondences between 3D shapes is an im- portant and long-standing problem in computer vision, graphics and beyond. A prominent challenge are partial- to-partial shape matching settings, which occur when the shapes to match are only observed incompletely (e.g. from 3D scanning). Although partial-to-partial matching is a highly relevant setting in practice, it is rarely explored. Our work bridges the gap between existing (rather artificial) 3D full shape matching and partial-to-partial real-world set- tings by exploiting geometric consistency as a strong con- straint. 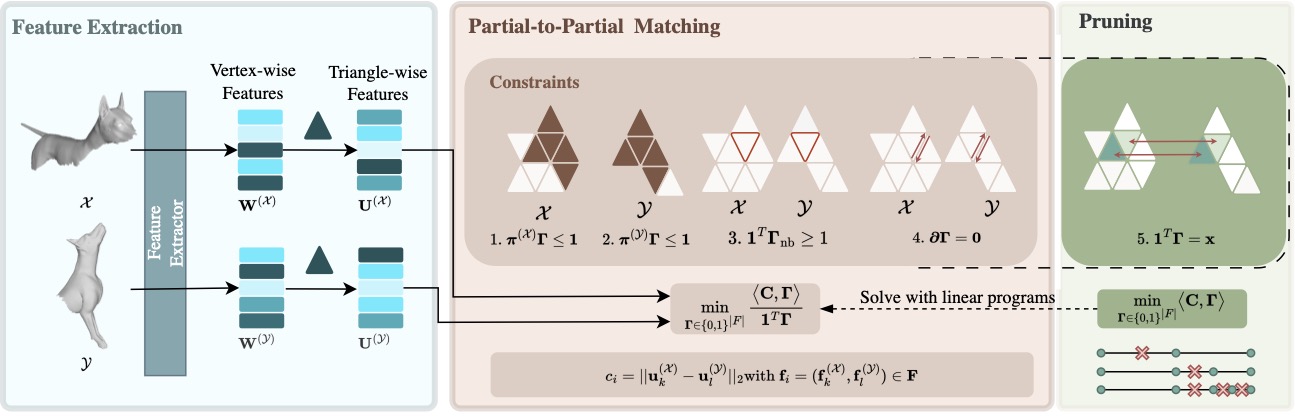We demonstrate that it is indeed possible to solve this challenging problem in a variety of settings. For the first time, we achieve geometric consistency for partial- to-partial matching, which is realized by a novel integer non-linear program formalism building on triangle prod- uct spaces, along with a new pruning algorithm based on linear integer programming. Further, we generate a new inter-class dataset for partial-to-partial shape-matching. We show that our method outperforms current SOTA meth- ods on both an established intra-class dataset and our novel inter-class dataset.

Overview



Our Partial-to-Partial Shape Matching Pipeline. (Left) The 3D meshes are fed into a feature extractor that returns vertex-wise features, that are transformed in trianglewise features. (Middle) With these features, we define an integer program that ensures that every triangle is matched at most once for both shapes, that at least one non-boundary triangle is matched (per shape), and that neighboring relationships for inner triangles are fulfilled. (Right) We tackle this non-linear integer program by solving a subset of integer linear programs (ILPs) for a specific number of matchings.

Citation